P value fallacy and misconceptions
04 Dec 2018

Definition of p-value
- P value is frequently used as a metric to evaluate significance of hypothesis testings
- It is the probability of observing the same or greater statistical summary than actual observed results, given that the null hypothesis is true
- It is used as a determinator to reject the null hypothesis; the less the p-value, the less the probability of getting the observed results is. This is why null hypothesis is rejected if p-value is low.
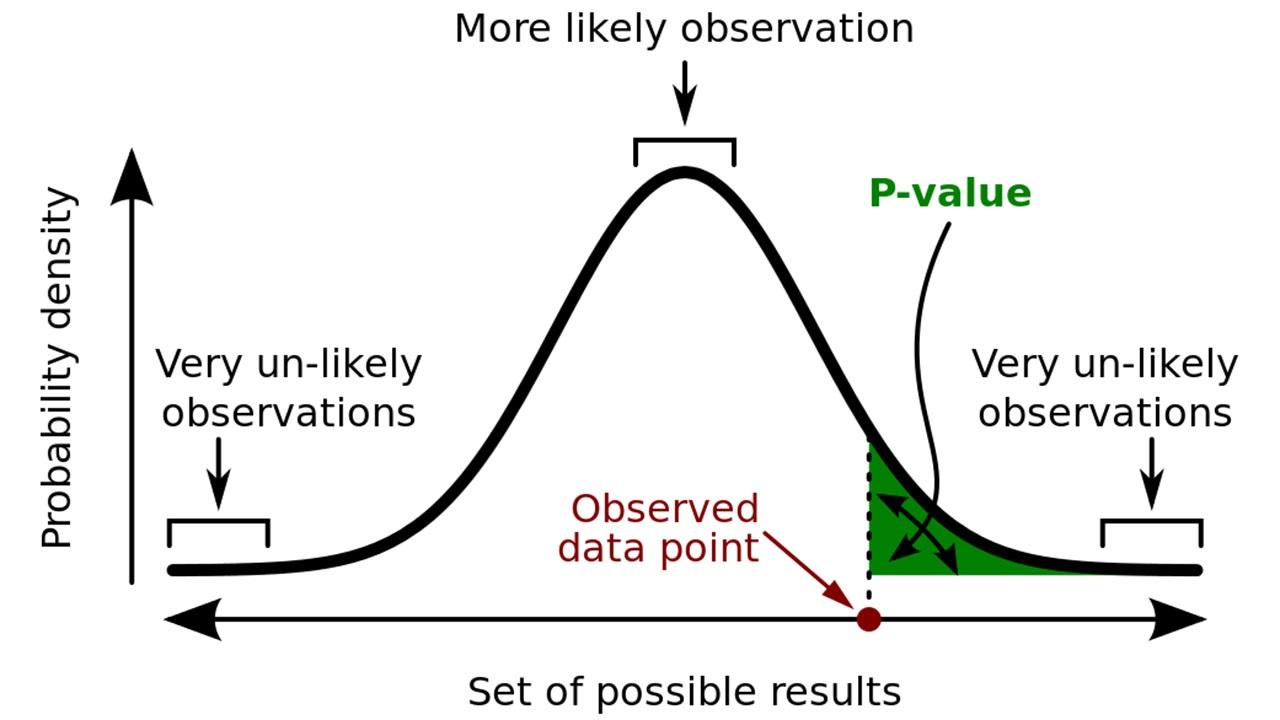
Misconceptions
P value is often used as a metric to show how significant the results of experiments are. However, the misunderstandings of p-values are prevalent many scientific research and scientific educations. This made the American Statistical Association release statement on p-values and statistical significance.
The following is the definition of p-value in the statement of ASA:
“Informally, p-value is the probability under a specified statistical model that a statistical summary of the data (e.g., the sample mean difference between two compared groups) would be equal to or more extreme than its observed value.”
These are some common misconceptions regarding p-values:
-
P-value is not a probability that the null hypothesis is true or the probability that the alternative hypothesis is false
-
P-value is not the probability that the observed effects were produced by random selection
-
The 0.05 significance level is merely a convention
-
P-value does not indicate the size or importance of the observed effect
Transposed Conditional Fallacy
According to the definition, p-value refers to the probability of observing a result given that some hypothesis is true. In a mathematical expression:
$$ P(Observation \vert Hypothesis = True ) $$
However, p-value is erroneously used as a “score” or “index” to assess the true or false of a hypothesis:
$$ P( Hypothesis = True \vert Observation ) $$
Since the two expressions are different, misunderstanding these two conceptions will cause conditional probability fallacy.
Principles to have in mind when using p-values
Many research use p-value to test the true or false of their model or classify results. However, p-value cannot be a sole evidence that concludes the viability of research or model. Here are the principles that ASA strongly advise when using p-values:
- P-values can indicate how incompatible the data are with a specified statistical model.
- P-values do not measure the probability that the studied hypothesis is true, or the probability that the data were produced by random chance alone
- Scientific conclusions and business or policy decisions should not be based only on whether a p0value passes a specific threshold
- Proper inference requires full reporting and transparency
- A p-value, or statistical significance does not measure the size of an effect or the importance of a result
- By itself, a p-value does not provide a good measure of evidence regarding a model or hypothesis
In a gist, p-value is not a panacea to statistical inference or model development. Scientists or data analyst must not selectively pick the p-value that supports their desirable outcome. In order to verify results of research, they should be reproducible: other scientists or researchers should be able to produce similar or consistent result using the same methodology. P-value is only one cause of the reproducibility crisis. For the development of science, the false conventional use of p-values or statistical significance must be refrained.
References
- Wasserstein, R. L. & Lazar, N. A. advance online publication The American Statistician (2016); http://www.amstat.org/newsroom/pressreleases/P-ValueStatement.pdf
- http://www.nature.com/news/reproducibility-1.17552
- http://www.nature.com/news/how-scientists-fool-themselves-and-how-they-can-stop-1.18517
- http://www.nature.com/news/statistics-p-values-are-just-the-tip-of-the-iceberg-1.17412
- http://www.ibric.org/myboard/read.php?Board=news&id=270293
- http://www.nature.com/news/psychology-journal-bans-p-values-1.17001
Error vs Residual
24 Nov 2018

To be honest, I have always had problems with terminologies used in Statistics. Because they sound to similar and they are expressed in similar ways, it is quite confusing. One of the confusing concepts was difference between error and residual.
Error (Disturbance) - $\varepsilon , \epsilon$
In a simple way to put this, statistical error is the difference between observed value and true value (unobservable in most situations). The whole purpose of inferential statistics is to find properties of population using your data.
Error is the quantity that tells how much the truth or values in population deviate from a true model. In Statistics, error is inevitable. Your observations cannot be 100% true, because how you collect data can defintely influence the observations. These types of errors are more involved with observational error.
Let’s look at a simple linear regression equation below:
$Y_i = \beta_1 + \beta_2X_i + \epsilon_i$
We can write this as a matrix form:
\[\bold{y} = \begin{pmatrix} y_1 \\ y_2 \\ y_3 \\ . \\ . \\ \end{pmatrix},\ \bold{X}= \begin{pmatrix} 1 &x_1 \\ 1 & x_2 \\ 1 & x_3 \\ . & . \\ . &. \\ \end{pmatrix}, \ \bold{B} =\begin{pmatrix} \beta_1 \\ \beta_2\end{pmatrix} , \ \bold{\varepsilon} = \begin{pmatrix} \epsilon_1 \\ \epsilon_2 \\ \epsilon_3 \\ . \\ . \\ \end{pmatrix}\]
$\bold{\varepsilon} = \bold{y} - \bold{X}\bold{B}$
The error term $\epsilon_i$ is used to capture the difference between actual true value and the true linear model or true fit line ($\beta_1 + \beta_2X_i$) . It would be easier to think of these terms as “theoretical”. You don’t know them and cannot get them. This is because we don’t have all data points from the population. However, we are going to use our observations to estimate the model and error.
Residual - $r_i$
Residual is an estimate of error. It is an “observable estimate” of unobservable statistical error”1. Because we don’t know the true model, we cannot calculate the error either. So we estimate the two parameters of linear model ($\hat{\beta_1}, \hat{\beta_2}$) and calculate estimate of errors.
$Y_i = \hat{\beta_1} + \hat{\beta_2}X_i + r_i$
We can write this as a matrix form:
\[\bold{y} = \begin{pmatrix} y_1 \\ y_2 \\ y_3 \\ . \\ . \\ y_n \end{pmatrix},\ \bold{X}= \begin{pmatrix} 1 &x_1 \\ 1 & x_2 \\ 1 & x_3 \\ . & . \\ . &. \\ 1 & x_n\\ \end{pmatrix}, \ \bold{\hat{B}} =\begin{pmatrix} \hat{\beta_1} \\ \hat{\beta_2}\end{pmatrix} , \ \bold{r} = \begin{pmatrix} r_1 \\ r_2 \\ r_3 \\ . \\ . \\ r_n \end{pmatrix}\]
$\bold{r} = \bold{y} - \bold{X}\bold{\hat{B}}$
Notice that $\bold{y}$ is not the same as the one on the error. Although residuals are different from errors, the two terms are somewhat used interchangeably, because they are used instead of errors. We use residuals to find out what information has not been captured by our model.
 source = “https://www.youtube.com/watch?v=snG7sa5CcJQ”
source = “https://www.youtube.com/watch?v=snG7sa5CcJQ”
1 https://en.wikipedia.org/wiki/Errors_and_residuals
Misunderstanding Correlation & Base Rate Fallacy
22 Nov 2018

Correlation does not imply Causation
 source: https://www.statisticshowto.datasciencecentral.com/spurious-correlation/
source: https://www.statisticshowto.datasciencecentral.com/spurious-correlation/
“We can definitely save astronaut’s life by using seatbelts in the car!”
You would probably laugh at this statement, because it is pretty obvious that this is a spurious correlation. Many research papers and people make mistakes by associating correlation with causality.
“Correlation does not imply causation”. It does not guarantee anything, but only shows a possibility
A. Strong positive correlation between annual ice-cream sales and number of drownings
B. Strong positive correlation between number of bars and churches in the city
C. Strong positive correlation between life expenctancy and hormone supplements for middle aged
The following correlations above are all fallacious. More logical reason or cause of A would be seasonal changes. You would eat more ice cream and swim on the hot summer than in the cold winter. B is just an observation based on different size of cities. Of course you would have more churches and bars in New York than in Alaska. C is a bit tricky, but “money” turns out to be the causal factor behind this correlation. The richer you are, the more you can afford to spend on your health.
Likewise, high correlation fools us to think that there is an actual casual relationship between the two variables. Here are some types of correlation mistakes:
-
Spurious Correlation
All the examples that we have talked about above, is spurious correlation. This is a deceptive association due to some other variables in between them. Season, size of the city, money were the hidden key variables in these cases.
-
Coincidental Correlation
“Annual number of people drowned by falling into a swimming pool has high correlation with the annual number of films Nicholas Cage appeared in”. The two figures are just a coincidence. We cannot blame Nicholas Cage for the death of all drowned people in the swimming pool. This is what we call coincidental correlation.
Once again, Correlation does not lead to Causation. So, be careful with your correlation coefficient.
Also, try to think about the images below.


Base Rate Fallacy (Base Rate Neglect)
Base rate fallacy is another logical error that we are often exposed to. We are prone to jumping into conclusions without thinking about the whole picture. This happens when we make irrational decisions based on our bias or belief, in favor of statistical probability or ignore general .
Base rate is the probability of event also known as prior probabilities in Bayesian term. In an easy way to put this, it is “a percentage of a population that demonstrates some characteristics”1. Obviously, when base rate is ignored or neglected, fallacy occurs. Here’s an example:
-
0.5% of students cheat on their quiz
-
Teachers catch cheaters with a 5% false positive rate (type 1 error; caught cheating but innocent in fact)
-
Teachers examine all 1000 students taking their quiz
Now, Michael is caught by teachers as a cheater. What would be the chance that he is innocent?
Base rate fallacy occurs when people think that Michael is innocent by 5%, only considering information on the second bullet point.
In fact, 1000 students will be examined. Among these students only 5 students will cheat(the base rate), but the teachers will catch 50 students as cheaters. In this sense, Mike will be innocent by 90% (45/50) chance.
Most smart women with very high IQ scores date someone else dumber than them
Now we all know that this is not surprising if we think of the base rate; super smart women are more likely to encounter people dumber than them.
References
1 https://link.springer.com/referenceworkentry/10.1007%2F978-0-387-79061-9_289
Logistic Regression
15 Nov 2018

-
Logistic Model is a statistical model that uses a logistic function to classify dependent variable.
-
In general, (Binary) Logistic Regression is used for binary classification. (Pass/Fail, Alive/Dead, Win/Lose, etc…) If there are more numbers of dependent variables, you should look into multinomial logistic regression
-
As its purpose is mainly in binary classification, the model is often used for supervised machine learning.
-
The dependent variables are labeled as 0 or 1.
-
If the probability of predicting dependent variable to 0 is above 50%, the dependent variable will be classified as 0. Else, it would be classified as 1.
The Logistic Model derived from linear regression. If we set y as the probability of predicting one of the two dependent variables, classification becomes easy.
If y > 0.5, it will be labeled as dependent variable A. If y < 0.5, it will be labeled as dependent variable B.
\[y = ax+b\]
However, as we can see from the linear regression model above, y and x can have infinite values. As the name suggests, the logistic model is derived from the linear equation by transforming it with logit function.
Logit Function
Logit function, or log-odds is the logarithm of the odds(relative probability the event will happen)
\(odds : \frac{p}{1-p}\)
p is the probability that the event will happen. Thus, the logit function and inverse logit function is:
\[logit(p)= ln\frac{p}{1-p}\]
Logistic Function
Using the logit function, the linear model can be transformed as following equation:
\(logit(p)= ln\frac{p}{1-p}= ax + b\)
\(\frac{1-p}{p}= \frac{1}{e^{ax+b}}\)
\(p= \frac{e^{ax+b}}{e^{ax+b}+1}\)
How to Use it on Python
Let’s get into some practical stuff now. The code for logistic regression is pretty short and simple. You just need training dataset and testing dataset to build a model.
from sklearn.linear_model import LogisticRegression
# Calling the function and training data
lg = LogisticRegression() #make an instance of the Model
lg.fit(x_train, y_train) #fit your training dataset
# Making predictions and calculating accuracy
predictions = lg.predict(x_test) # Predictions
accr = lg.score(x_test, y_test) # Accuracy
print(predictions)
print(accr)
Basic SQL Grammar
04 Nov 2018

SQL (to be Updated)
- Structured Query Language (SQL), is a programming language used to manage or process data in Relational Database Management System (RDBMS)
- SQL is useful in handling structured data that includes relations between different data tables
- SQL is used to create, manage, query, manipulate the data with statements
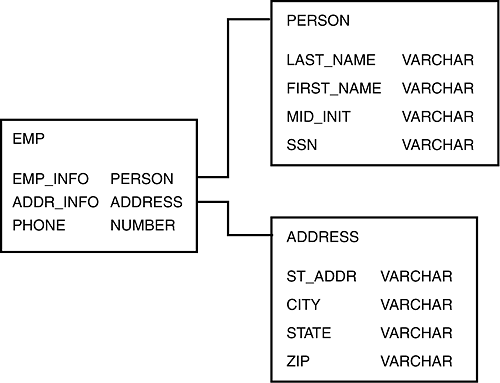 img source: https://medium.com/@swiftsnippets/database-system-s-rdbms-and-nosql-6afeef8168e5
img source: https://medium.com/@swiftsnippets/database-system-s-rdbms-and-nosql-6afeef8168e5
Basic Statements
SELECT
SELECT is used to select data from a database (most statements are self-explanatory…)
SELECT column1, column2, …
FROM table_name;
If you want to select all columns, simply use * (asterisk)
SELECT * FROM table_name;
If you want to select only unique or different values, use DISTINCT
SELECT DISTINCT column1, column2, …
FROM table_name;
If you want to select values with certain conditions, use WHERE
SELECT column1, column2, …
FROM table_name
WHERE condition;
The following are operations that can be used with the WHERE clause:
| Operator |
Description |
| = |
equal |
| <> or != |
not equal |
| < |
less than |
| > |
greater than |
| BETWEEN |
between a range |
| LIKE |
pattern search |
| IN |
specify multiple values
as an inclusive syntax |
Example
SELECT DISTINCT * FROM product_info WHERE price > 40;
AND, OR, NOT
AND, OR, and NOT operators are combined with other statements to filter records in a more desirably way. It is used in a similar manner just as in other programming languages.
- AND displays a record if all the conditions stated and connected with AND are TRUE
- OR displays a record if any conditions stated with OR are TRUE
- NOT displays a record if the conditions is NOT TRUE
Examples
SELECT *
FROM product_info
WHERE price BETWEEN 20 AND 30
SELECT *
FROM product_info
WHERE color = “red” OR “blue”



 source = “https://www.youtube.com/watch?v=snG7sa5CcJQ”
source = “https://www.youtube.com/watch?v=snG7sa5CcJQ” source: https://www.statisticshowto.datasciencecentral.com/spurious-correlation/
source: https://www.statisticshowto.datasciencecentral.com/spurious-correlation/

