Regularization

04 Feb 2020

Supervised Learning can be explained as a process of finding the optimal weights of input features (predictors) to get the pre-determined outcome (labels). We tune hyperparameters, preprocess data and incorporate statistical methods to calculate weight of each variables that you feed to the model.

Meanwhile, one of the most important concerns when training a Machine Learning model is overfitting. This happens when your model is too complex that it performs extremely well on the train set, but poorly on the test set.

The image below illustrates an intuitive difference between a complex model (blue line) and a simple model (green line).

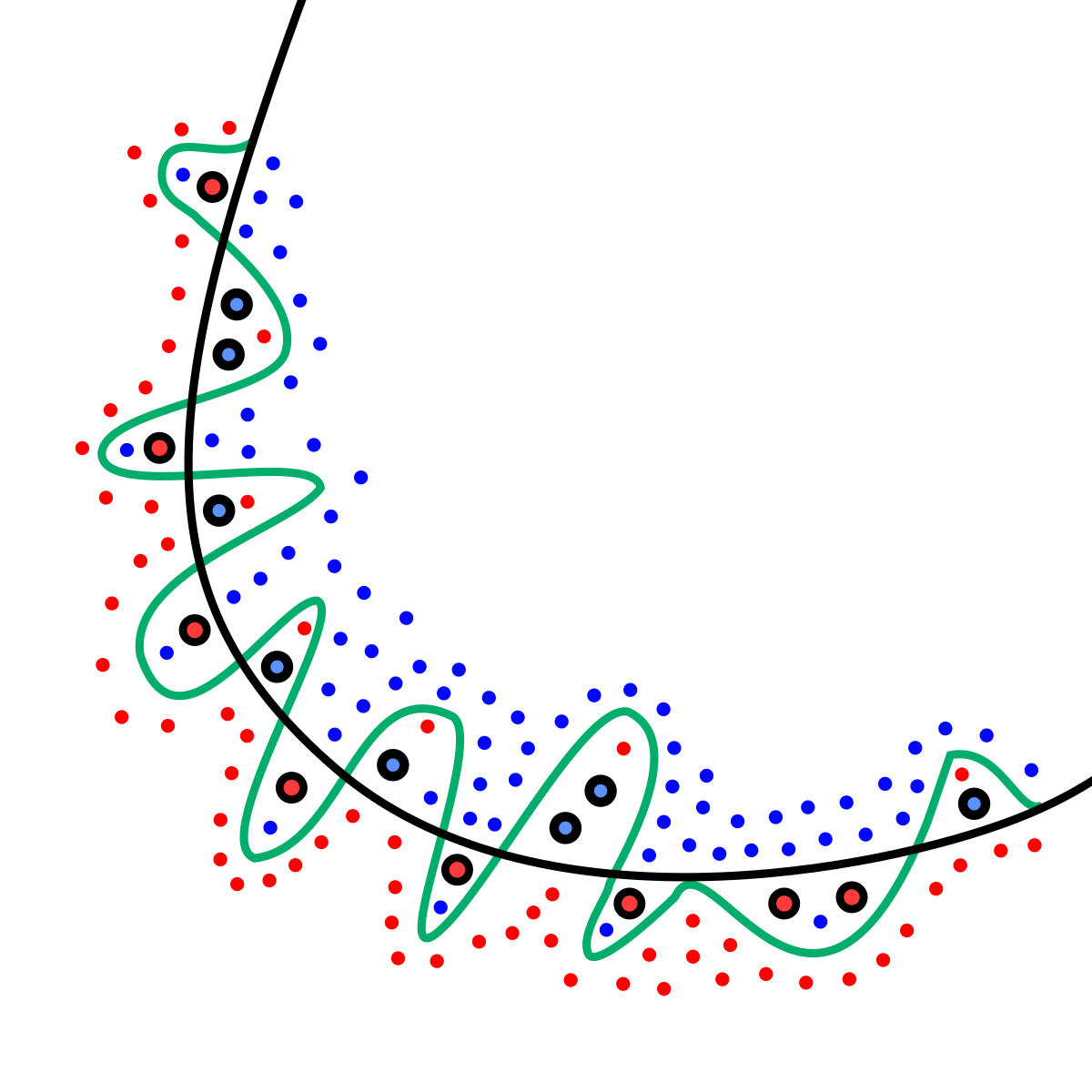
There are various methods that have been studied to prevent overfitting, which includes hyperparameter tuning, cross-validation, selecting features, and ensembling. Among the techniques, a way to fight overfitting by directly referring to the weights is called regularization.

Regularization

Overfitting is relevant to the number of weights or the size of weights. The number of weights implies the number of variables we are using for feeding the model. As we use more variables in the model, the dimension of weight space will increase as well as the complexity of the model. Small size of weights are also desirable to prevent overfitting, because large weights can cause rapid change in the model just like the green curve.

The bottom-line of how regularization works is that it punishes the loss function by taking number or size of weights into account. Of course, the method varies by how it penalizes the loss function

$L_0, L_1, L_2$ Regularization

The name of $L_0, L_1, L_2$ regularization is derived from the types norm applied to the weight vector. The penalization is done by adding these terms to the loss function.

In general, we define model as :

\(\hat{y} = \textbf{w}^T\textbf{x}\),

• $\textbf{w} = (w_1,w_2,w_3,…w_n)$ : weight vector
• $\textbf{x} = (x_1,x_2,x_3,…x_n)$ : vector of selected features or variables.
• $f$: loss function

The loss would be $f(y - \hat{y}) = f(y-\textbf{w}^T\textbf{x})$ and minimizing this would be the objective of machine learning. The regularization modifies this loss by adding the norm:

\[f(y - \textbf{w}^T\textbf{x}) + \lambda\times norm\]

($\lambda$ is the degree of penalization or strength of regularization. This is also a hyperparameter.)

$L_0$ norm​ ($\vert\vert\textbf{w}\vert\vert_0$) is the number of non-zero elements in a vector:

$L_0 \ regularization = f(y - \textbf{w}^T\textbf{x}) + \lambda \vert\vert \textbf{w}\vert\vert_0$

$L_1$ norm ($\vert\vert\textbf{w}\vert\vert_1$) is the sum of absolute values in a vector:

$L_1 \ regularization = f(y - \textbf{w}^T\textbf{x}) + \lambda\vert\vert\textbf{w}\vert\vert_1$

$L_2$ norm ($\vert\vert\textbf{w}\vert\vert_2$) is the squared root of the sum of squared values in a vector. $L_2$ regularization uses squared value of $L_2$ norm:

$L_2 \ regularization = f(y - \textbf{w}^T\textbf{x}) + \lambda\vert\vert\textbf{w}\vert\vert^2_2$

Intuitions & Comparison between Regularization Methods

• Using $L_1$ regularization in linear regression is called Lasso regression, while using $L_2$ regularization is called Ridge regression
• $L_0$ method promotes using less amount of features, so it can be used as a feature selection method.
• $L_1$ method encourages non-necessary feature weights to be zero. As you strengthen the regularization power (increasing $\lambda$), features with small weights will be zero. Thus, we can use $L_1$ regularization as feature selection, just like $L_0$. Also, $L_1$ is more robust than $L_2$ because it is less sensitive to outliers. However, $L_1$ does not have a unique solution.
• $L_2$ method is less sensitive to data compared to $L_1$. Sensitive here means that the weights remain fairly consistent when there is a small adjustment to the data points. Also, because it is a convex the solution is unique when minimizing it. Thus it is computationally efficient. Unlike $L_0, L_1$, because $L_2$ does not completely make weights to 0, it can be a bit sensitive to irrelevant variable or features.
• In regularization scale and units of variables matter a lot.
• The overfitting occurs, because we do not have all data. Thus, the effect of regularization will go down as the training data size increases.

Elastic Net

Elastic net is a regularization method with $L_1$ and $L_2$ combined:

$f(y - \textbf{w}^T\textbf{x}) + \lambda(\alpha\vert\vert\textbf{w}\vert\vert_0+ (1-\alpha)\vert\vert\textbf{w}\vert\vert^2_2)$

• $\lambda$ control the strength of regularization

• $\alpha$ controls the relative strength of each regularization method
• L1 promotes sparsity (less weight number) and the L2 promotes smoothness.
• The functional is strictly convex, so the solution is unique.