Jaekeun Lee's Space     Projects     About Me     Blog     Writings     Tags

Linear Algebra Terminology

20 Jun 2019 Tags:
Linear Algebra, Linear Independence, Linear Combination, Span



Span, Linear Combination, Linear Independence


  • Linear combination is vectors expressed by scalar multiplication or addition of vectors.

  • Span (or Linear Span) of a set of vectors is the set of all linear combinations of those vectors.

  • A set of vectors are linearly independent, only if all vectors contribute to their span. In other words, removing one of the vectors from the set would affect the span.


Definitions of linear combination, span and linear independence have been given above. However, these definitions are not very intuitive or give us a clear picture of what they mean. Here, I will attempt to provide visual and geometrical implication of these definitions.


Linear Combination



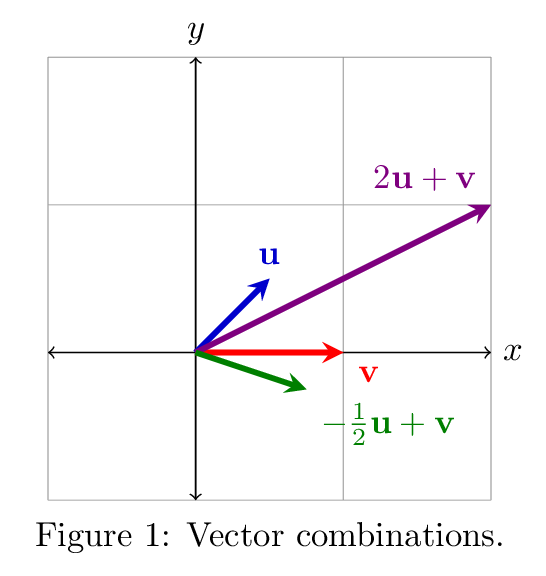
The illustration above shows two results of combination of $\vec{u}$ and $\vec{v}$. Linear combination refers to addition of vectors that are multiplied by some numbers (or scalars). The purple and green vectors can be seen as a linear combination of $\vec{u}$ and $\vec{v}$.

In general, linear combination can be expressed as an expression below:

$a_1\vec{x_1}+a_2\vec{x_2} +a_3\vec{x_3}+a_4\vec{x_4}+… a_n\vec{x_n} $


Span



Span of vectors can be viewed as a collection of all linear combinations of those vectors. For example, the span of red and blue vector ($\vec{u}$ and $\vec{v}$) from the illustration above will a collection of the green vectors (linear combinations of $\vec{u}$ and $\vec{v}$), which will form the pink plane (the span of $\vec{u}$ and $\vec{v}$)


Linear Independence


Imagine a linear combination of two vectors that have same direction, but different in their scale. What would their span look like?

From the previous illustration, we can easily see that the span would look like a straight line. For example, the red line that vector $\vec{u}$ and $2\vec{u}$ spans, or the blue line that the blue vector $\vec{v}$ and $2\vec{v}$ spans. However, these lines can be spanned without $2\vec{u}$ or $2\vec{v}$. $\vec{u}$ and $\vec{v}$ are sufficient enough to span these lines. This is where the definition of linear independence kicks in.

We can say that a set of vectors are linearly independent, only when the respective vectors are not a linear combination of any pairs of remaining vectors.



On the right, $\vec{w}$ is a linear combination of $\vec{u}$ and $\vec{v}$, whereas on the left $\vec{w}$ cannot be represented by a linear combination of $\vec{u}$ and $\vec{v}$. So, the left is the case when we can say that $\vec{u},\ \vec{v}$ and $\vec{w}$ are linearly independent.

Reference

https://www.youtube.com/watch?v=k7RM-ot2NWY&list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab&index=2

Related Posts