InfoGAN

Information Maximizing Generative Adversarial Network (InfoGAN) attempts to learn disentangled representations by maximizing mutual information cost. It introduces a simple add-on on GAN to fulfill its purpose. The key idea is to insert a latent code that represents specific feature in a Generative Model and maximize the mutual information between the code and the generated distribution.

…. Let’s try to understand these sentences above. First, let’s look at the context behind this GAN.

The Context Behind InfoGAN

Measuring Information

Information in general terms is defined as facts about a situation, person, events, etc. It plays a crucial role in making decisions, solving various problems and adapt to changes. As much as it is important, devising a way to measure and quantify information is also neccessary. So, how can we measure information?

This is done by a field of science called information theory, which aims to study the quantification, storage and communication of information. Information theory was proposed by Claude Shannon in his seminal paper “A Mathematical Theory of Communication”, where he introduced the concept information entropy: a method to measure information.

Information Content, Information Entropy, Mutual Information

Information content (=surprisal) is defined as the amount of information gained when it is sampled. The core idea behind this is that unlikely event (events with less probability) has more amount of information than the more likely event (events with higher probability). Because information that everyone knows is not highly valuable, high probability of event would carry less information then an event with low probability. In this sense, information content is defined as:

$Information\ content: I(x) = -logP(x) ​$

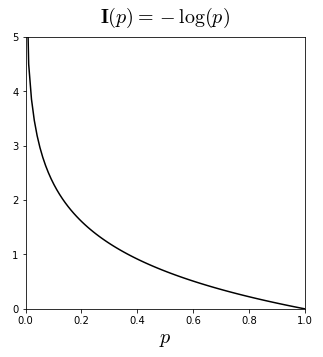
Meanwhile, the keyword of information theory is “entropy”. Entropy measures the uncertainty of situation in physics. The definition of information entropy is “the expectation at which information is produced by a stochastic source of data”. Thus, in relevance to the mathematical statistics, expectation of information content would be the information entropy, or Shannon entropy:

​ \(H(x) = - \sum_{i} P_{i}logP_{i}\)

Mutual Information quantifies the amount of information learned from knowledge of one random variable about the other random variable. If the two random variables are independent, information of a random variable cannot be obtained by knowing the other random variable. For example, knowing that a flipped coin was a tail, does not give any information about whether it would rain tommorow or not. In this context, mutual information of X, Y would be 0 if the two variables are independent. The mutual information of can be expressed using the difference of Shannon entropy in conditional aspect:

Disentangled Representation

Disentangled representation refers to the idea of disentangling a highly entangled data; most data includes representation of features, but they are entangled in a complicated manner, thus it is hard to identify these features on a seperate term.

For example, let’s say that there is an image of cat. The image of cat itself is highly entangled data of various representative features such as whiskers, triangular ears, tails, nose, etc. If unsupervised machine can learn these representations seperately, it would be able to produce better results.

The figure below is an excellent example of disentagled representation:

source: https://www.slideshare.net/ssuser06e0c5/infogan-interpretable-representation-learning-by-information-maximizing-generative-adversarial-nets-72268213

InfoGAN

So far, we have skimmed through the background knowledge involving Information Maximization GAN. Finally we can talk about how InfoGAN works.