Student's T-test

Student’s T-Test

• Student’s t-test is one of statistical hypothesis tests which is performed when the test statistics is assumed to follow a Student’s t-distribution under the null hypothesis.
• It is usually used to compare means of two samples to see if they are equal or not.
• There are different types of t-test, so we should be aware of which t-test to choose.

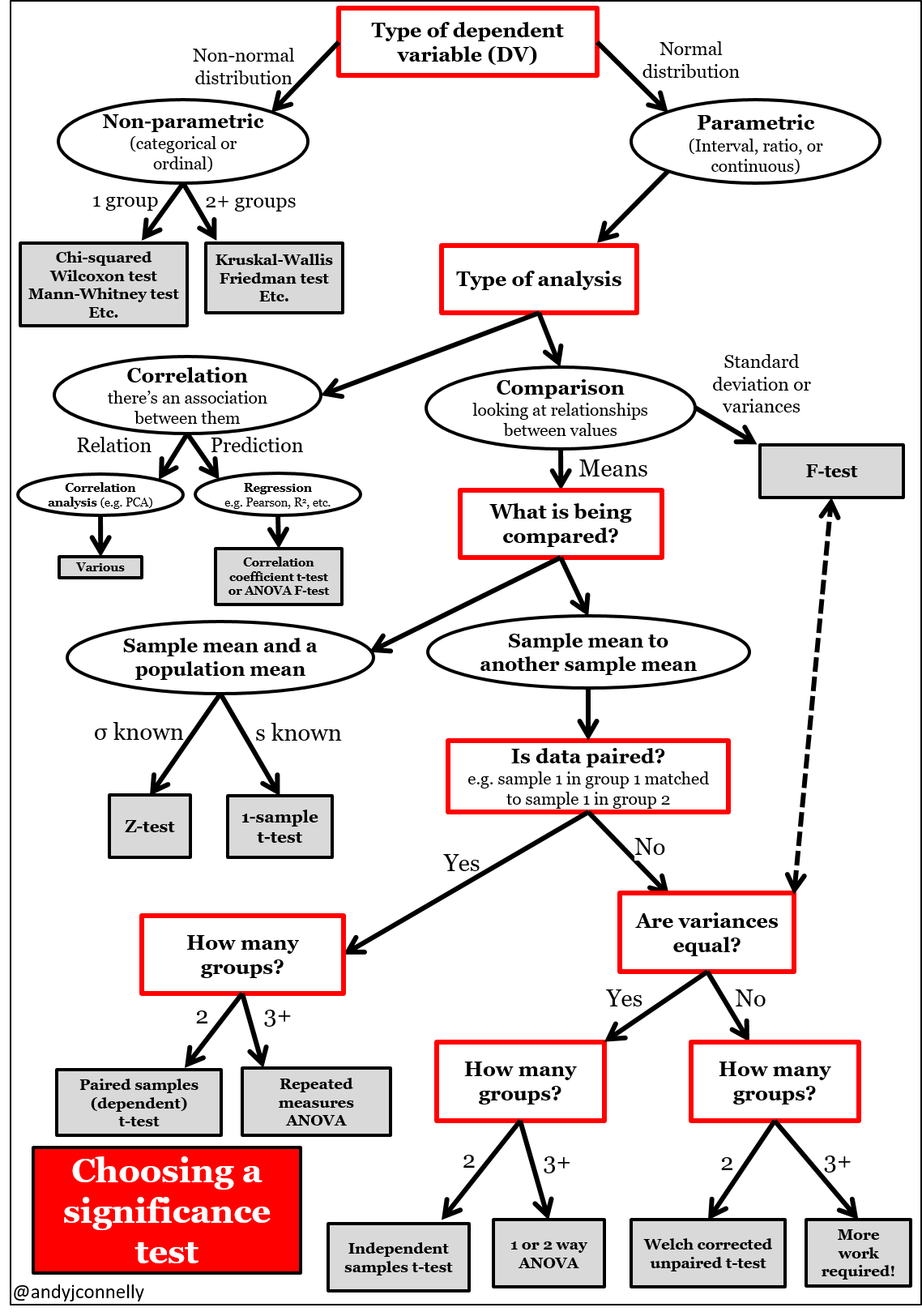
The diagram above briefly shows which significance test to choose from, when you perform statistical hypothesis tests. You can see several types of t-tests, but in this post I will only cover the most fundamental t-tests that are used for comparing two sampes: paired(dependent) t-test, unpaired(independent) t-test

Unpaired t-test

    Unpaired t-test assumes that two sample groups are independent and from an approximately normal distribution. The formula differs depending on the equivalence or variance.

Equal variance

  parameters:

• \(\bar{x_1}, \bar{x_2}\) is mean value of group 1 and group 2

• \(n_1, n_2\) are numbers of samples of group 1 and group 2

• t-test statistics value: \(t = \frac{\bar{x_{1}}+\bar{x_{2}}}{\sqrt {s^2\biggl(\frac{1}{n_{1}}+\frac{1}{n_{2}}\biggr)}}\)
  

• pooled sample variance: \(s^2 = {\sum_{i=1}^{n_1} (x_i - \bar{x_1})^2 + \sum_{j=1}^{n_2} (x_j - \bar{x_2})^2\over n_1 + n_2 - 2}\)

• degree of freedom: \(df = n-1\)

R Code

t.test(x, y, alternative = "two.sided", var.equal = TRUE)

# or

t.test(dataset$y1, dataset$y2, data = my_data, var.equal = TRUE)

Non-equal variance

  parameters:

• t-test statistics value: \(d = \frac{\bar{x_1}+\bar{x_2}}{\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}\)
  

• group 1 sample variance: \(s_1 = \frac{\sum_{i=1}^{n_1} (x_i - \bar{x_1})^2}{n_1 -1}\)

• group 2 sample variance: \(s_2 = \frac{\sum_{j=1}^{n_2} (x_j - \bar{x_2})^2}{n_2 -1}\)

• degree of freedom: \(df = {\biggl[\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}\biggr]\over {\bigl(\frac{s_1^2}{n_1}\bigr)^2\over n_1 - 1} + {\bigl(\frac{s_2^2}{n_2}\bigr)^2\over n_2 - 1} }\)

R Code

t.test(x, y, alternative = "two.sided", var.equal = FALSE)

# or

t.test(dataset$y1, dataset$y2, data = my_data, var.equal = FALSE)

Paired t-test

    Unlike, unpaired t-test, paired t-test is used to compare sample menas of two related(dependent) groups (ex. pair of values; before & after)

parameters:

• t-test statistics value: \(t = \frac{m}{\frac{s}{\sqrt n}}\)
  • \(m\) is the mean difference between two groups
  • \(n\) is the sample size of \(d\)
  • \(s\) is the standard devidation of \(d\)
• \(df\)(degree of freedom) is \(n-1\)

R Code

t.test (Y ~ X, dataset, paired=TRUE)

# or 

t.test(dataset$y1, dataset$y2, paired=TRUE)