Jaekeun Lee's Space     Projects     About Me     Blog     Writings     Tags

Multiprocessing with Python

25 Apr 2020 Tags:
Parallel processing, Multiprocessing, Python


Handling Big Data

Working with big data is a stressful job, especially when it involves a massive amount of computation. For example, training neural networks or dealing with gigabytes of data would be time-consuming. When it comes to enhancing the performance speed of high complexity tasks, there are two approaches: Vertical Scaling and Horizontal Scaling.

Vertical Scaling is an approach that refers to adding more power to the existing computing power. Buying better hardware using it can ensure faster computing. Instead of delivering many packages with a single bike, using a truck would be more efficient.

Horizontal Scaling uses more computing instances to tackle this problem. By dividing the work and assigning it to multiple computers, the task can be finished faster. Think of it as dividing packages and delivering them with multiple bicycles.

In this post, we will talk about parallel processing which is a horizontal scaling approach to solve tasks with high time complexity.


Multiprocessing

Python has a bult-in function called multiprocessing . The module enables users to perform their tasks in a parallel manner by taking advantage of multi-core CPUs.

Let’s take a look at the code below:


Sequential Processing

import time

# starting time
start = time.time()

# save the factorial results here
s_results = []

# add all integers from 1 to 1_000_000
def factorial(i):
    x = 1
    for k in range(1,i+1):
        x = x*k
    results.append(x)

# number of test cases
cases = [x for x in range(0,2001)]
for c in cases:
    factorial(c)

print("%s seconds" % (time.time()-start))

> 0.5778999328613281 seconds


Parallel Processing (using multiprocessing library)

import multiprocessing as mp
import time

# starting time
start = time.time()

# save the factorial results here
p_results = []

# calculate factorial of a number
def factorial(i):
    x = 1
    for k in range(1,i+1):
        x = x*k
    p_results.append(x)

# factorials from 1 to 2000
cases = [x for x in range(1,2001)]

######################
### The Difference ###
pool = mp.Pool(processes=5) # Number of processes that you want to use
pool.map(factorial, cases)
pool.close()
pool.join()
######################

print("%s seconds" % (time.time()-start))

> 0.222374095917 seconds


Confirming the results are equal

s_results == p_results

> True


However, parallel processing is not always faster than serial processing. The performance depends on the number of iterations. Parallel programming is efficient when each iteration is sufficiently expensive compared to processor time


Comparing sequential and parallel running time of factorial() (Optional)

Let’s prove whether parallel programming is not always faster than sequential programming:

Create running time data for comparison (This takes a while; took me about 20 minutes to run)

import multiprocessing as mp
import time

# calculate factorial of a number
def factorial(i):
    x = 1
    for k in range(1,i+1):
        x = x*k

# measuring computation time for seq and parallel
seq_times = []
prl_times = []

for i in range(101,2501):
    cases = [x for x in range(1,i)]
  
  # Sequential
  # starting time
    seq_start = time.time()
    for c in cases:
        factorial(c)
    seq_times.append(time.time()-seq_start)
        
  # Parallel
    prl_start = time.time()
    pool = mp.Pool(processes=5) # Number of processes that you want to use
    pool.map(factorial, cases)
    pool.close()
    pool.join()
    prl_times.append(time.time()-prl_start)

import seaborn as sns
import pandas as pd

fac = [i for i in range(101,2501)]

df = pd.DataFrame(data={"upper limit":fac,
                        "sequential":seq_times,
                        "parallel":prl_times})

df = df.melt(id_vars="upper limit",value_name="time",var_name="processing type")

sns.set(rc={'figure.figsize':(15,8)})
ax = sns.lineplot(x=df["upper limit"], y=df["time"], hue=df["processing type"])
ax.axes.set_title("Sequential vs Parallel processing time of factorial() function",fontsize=18)
ax.set_xlabel("Upperbound of calculated factorials",fontsize=15)
ax.set_ylabel("Time (sec)",fontsize=15)


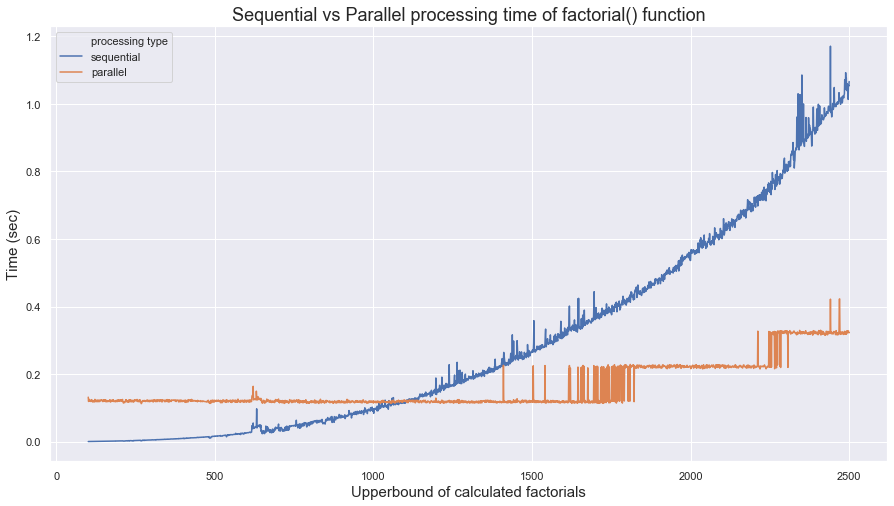
As shown in the output image above, parallel processing is faster than sequential processing when the number factorials required to compute exceeds approximately 1100. The takeaway here is that parallel processing is only useful when the computation load is sufficiently expensive compared to the processor time.

Related Posts